10142. Power
of time
There are n processes to be completed by you.
All the processes have a unique number assigned to them from 1 to n. You are given two things:
·
The calling order in which all the processes are
called.
·
The ideal order in which all the processes should
have been executed.
If the process in
the calling order cannot be executed (does not fit the ideal order), then it is
put to the end of the calling order queue for execution.
Now, let us
demonstrate this by an example. Let's say that there are 3 processes,
the calling order of the processes is: 3 – 2 – 1. The
ideal order is: 1 – 3 – 2, i.e.
process number 3 will only be executed after process
number 1 has been completed; process number 2 will only be
executed after process number 3 has been executed.
·
Iteration #1: Since the ideal order has
process #1 to be executed firstly, the calling ordered is changed,
i.e., the first element must be pushed to the last place. Changing the position
of the element takes 1 unit of time. The new calling order is: 2 – 1
– 3. Time taken in step #1: 1.
·
Iteration #2: Since the ideal order has
process #1 to be executed firstly, the calling ordered must be
changed again, i.e., the first element has to be
pushed to the last place. The new calling order is: 1 – 3 – 2.
Time taken in step #2: 1.
·
Iteration #3: Since the first element of the
calling order is same as the ideal order, that process will be executed. And it
will be thus popped out. Time taken in step #3: 1.
·
Iteration #4: Since the new first element of
the calling order is same as the ideal order, that process will be executed.
Time taken in step #4: 1.
·
Iteration #5: Since the last element of the
calling order is same as the ideal order, that process will be executed. Time
taken in step #5: 1.
Total time taken: 5 units.
Executing a
process takes 1 unit of time. Changing the position
takes 1 unit of time.
Input. First line contains the number of processes n (1 ≤ n ≤ 100). Second line contains the calling order of the
processes. The third line contains the ideal order of the processes.
Output. Print the total time taken for the entire
queue of processes to be executed.
|
Sample
input |
Sample
output |
|
3 3 2 1 1 3 2 |
5 |
SOLUTION
queue
Algorithm analysis
Declare two queues:
·
order contains the calling
order in which all the processes are called.
·
ideal contains the
ideal order in which all the processes should have been executed.
queue<int> order, ideal;
Then you should simulate
the queues:
·
If the process number in the head of the calling queue
coincides with the process number in the head of the ideal queue, then execute
the process and remove it from both queues.
·
Otherwise, the process should be removed from the head of the
calling queue and pushed to the end of this queue.
Example
Simulate the execution of
three processes from the example.
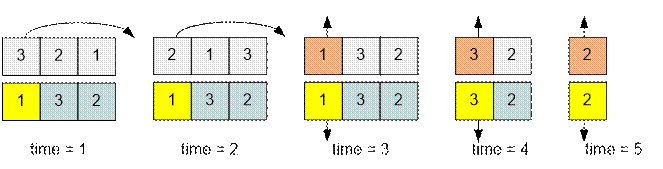
Algorithm realization
Declare two queues:
·
order contains the calling
order in which all the processes are called.
·
ideal contains the
ideal order in which all the processes should have been executed.
queue<int> order, ideal;
Read the number of processes n. Read the orders order and ideal.
scanf("%d", &n);
for (i = 0; i < n; i++)
{
scanf("%d", &x);
order.push(x);
}
for (i = 0; i < n; i++)
{
scanf("%d", &x);
ideal.push(x);
}
In the res variable count the
execution time of the processes.
res = 0;
Continue until all processes have been processed.
while (!ideal.empty())
{
res++;
If the process number in the head of the calling queue coincides with the
process number in the head of the ideal queue, then execute the process and
remove it from both queues.
if (order.front() == ideal.front())
{
order.pop();
ideal.pop();
}
else
{
Otherwise, the process should be removed from the head of the calling
queue and pushed to the end of this queue.
x = order.front(); order.pop();
order.push(x);
}
}
Print the answer.
printf("%d\n", res);
Java realization
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
Queue<Integer> order = new
LinkedList<Integer>();
for (int i = 0; i < n; i++)
{
int x = con.nextInt();
order.add(x);
}
Queue<Integer> ideal = new
LinkedList<Integer>();
for (int i = 0; i < n; i++)
{
int x = con.nextInt();
ideal.add(x);
}
int res = 0;
while (!ideal.isEmpty())
{
res++;
if (order.peek() == ideal.peek())
{
order.poll();
ideal.poll();
}
else
{
int x = order.poll();
order.add(x);
}
}
System.out.println(res);
con.close();
}
}